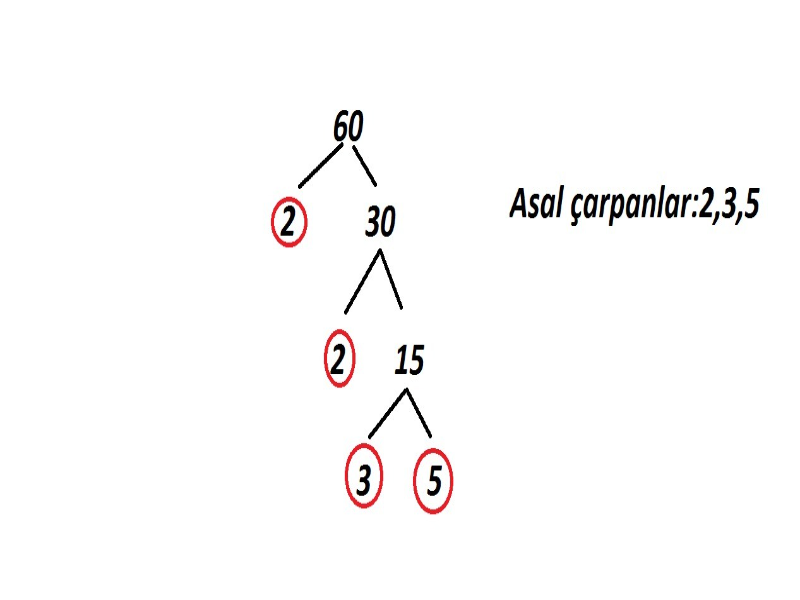
Asal çarpanlara ayırma, bir sayıyı yalnızca asal sayıların çarpımı olarak ifade etme sürecidir. Bu yöntem, matematikte sayıların temel yapı taşlarını anlamak için kritik bir rol oynar. Her bileşik sayı, asal çarpanlarına ayrılarak daha küçük asal sayılarla temsil edilebilir. Bu, sayıların özelliklerini incelemeyi ve matematiksel problemleri çözmeyi kolaylaştırır.

Bir sayıyı asal çarpanlarına ayırmak, o sayının en küçük asal sayılarla bölünmesiyle başlar. Herhangi bir bileşik sayı, birden fazla asal çarpanın çarpımı şeklinde ifade edilebilir. Örneğin, 60 sayısı 2, 3, ve 5 gibi asal çarpanların çarpımı olarak yazılabilir. Bu tür bir ayrıştırma, sayının yapısını derinlemesine anlamamızı sağlar.

Asal çarpanlara ayırma, matematiksel problemlerin çözümünde yaygın olarak kullanılır. Özellikle, sayı teorisi, kriptografi ve bilgisayar bilimi gibi alanlarda kritik öneme sahiptir. Bu yöntem, karmaşık hesaplamaları basitleştirmeye ve sayısal verilerin analizini kolaylaştırmaya yardımcı olur.

Asal Sayılar ve Önemi

Asal sayılar, yalnızca 1 ve kendisi ile bölünebilen pozitif tam sayılardır. Matematik dünyasında asal sayılar, sayıların yapı taşları olarak kabul edilir. Bu sayılar, diğer sayılardan farklı olarak, yalnızca kendileri ile çarpım yoluyla oluşturulabilir. Asal sayıların bu benzersiz özellikleri, onları matematiksel araştırmalarda vazgeçilmez kılar.

Asal sayıların önemi, birçok matematiksel teorinin temelini oluşturur. Örneğin, asal sayıların dağılımı üzerine yapılan araştırmalar, sayı teorisinin gelişmesine olanak tanımıştır. Ayrıca, asal sayılar, şifreleme sistemlerinde de kritik bir rol oynar. Kriptografi alanında, büyük asal sayılar kullanılarak güvenli şifreleme algoritmaları geliştirilir.

Asal sayılar, matematiksel problemlerin çözümünde ve algoritmaların geliştirilmesinde önemli bir yer tutar. Asal çarpanlara ayırma, asal sayıların özelliklerinden yararlanarak karmaşık problemlerin çözümünü basitleştirir. Bu nedenle, asal sayıların anlaşılması, matematiğin farklı alanlarında başarılı olmanın anahtarıdır.

Asal Çarpanların Bulunma Yöntemleri

Asal çarpanları bulmak için birkaç temel yöntem bulunmaktadır. Bunlardan biri, bölme yöntemi olarak bilinir. Bu yöntemde, sayıyı en küçük asal sayıdan başlayarak bölmeye çalışırız. Eğer sayı asal sayıya tam bölünüyorsa, bu asal sayı bir çarpan olarak kabul edilir ve bölme işlemine devam edilir.

Bir diğer yöntem, asal sayı listesi kullanarak asal çarpanları bulmaktır. Bu yaklaşımda, elinizde bir asal sayı listesi bulunur ve sayıyı bu listede yer alan asal sayılarla sırayla bölerek çarpanlarını bulursunuz. Asal sayı listesi, işlemi hızlandırır ve çarpanların doğru bir şekilde bulunmasını sağlar.

Çarpan ağaçları yöntemi ise görsel bir yaklaşımla asal çarpanları bulma tekniğidir. Bu yöntemde, sayıyı iki çarpana ayırarak bir ağaç yapısı oluşturursunuz. Her dal, sayının asal çarpanlarına ayrılmasını temsil eder. Bu yöntem, özellikle öğrencilerin asal çarpanları anlamasını kolaylaştıran bir tekniktir.

Asal Çarpanlara Ayırma Örnekleri

Asal çarpanlara ayırma sürecini anlamak için birkaç örnek inceleyelim. İlk olarak, 30 sayısını ele alalım. 30 sayısını asal çarpanlara ayırmak için en küçük asal sayı olan 2 ile bölmeye başlarız. 30 ÷ 2 = 15. 15 sayısı, en küçük asal sayı olan 3 ile bölünür. 15 ÷ 3 = 5. 5 ise asal bir sayıdır. Sonuç olarak, 30 = 2 × 3 × 5 şeklinde asal çarpanlarına ayrılır.

Bir diğer örnek olarak, 84 sayısını ele alalım. İlk olarak 2 ile bölerek başlıyoruz: 84 ÷ 2 = 42. 42 sayısı da 2 ile bölünebilir: 42 ÷ 2 = 21. 21 sayısı ise 3 ile bölünür: 21 ÷ 3 = 7. 7 ise asal bir sayıdır. Böylece 84 = 2 × 2 × 3 × 7 şeklinde asal çarpanlarına ayrılmış olur.

Son olarak, daha büyük bir sayı olan 120 sayısını ele alalım. 120, 2 ile bölünerek başlar: 120 ÷ 2 = 60. 60 sayısı da 2 ile bölünür: 60 ÷ 2 = 30. 30 sayısı da 2 ile bölünebilir: 30 ÷ 2 = 15. 15 sayısı 3 ile bölünebilir: 15 ÷ 3 = 5. 5 ise bir asal sayıdır. Böylece 120 = 2 × 2 × 2 × 3 × 5 şeklinde asal çarpanlara ayrılmış olur.

Asal Çarpanlara Ayırma ile İlgili Matematiksel Kurallar

Asal çarpanlara ayırma işlemi, belirli matematiksel kurallara dayanır. Bu kurallardan biri, her bileşik sayının asal çarpanlarına ayrılabileceğidir. Bu özellik, asal çarpanlara ayırmanın temel prensiplerinden biridir ve sayının asal çarpanlarının benzersiz olduğunu ifade eder.

Bir diğer kural, asal çarpanlara ayırma işlemi sırasında elde edilen çarpanların çarpımı, her zaman orijinal sayıya eşittir. Bu, işlemin doğruluğunu kontrol etmek için kullanılabilecek bir yöntemdir. Elde edilen çarpanların çarpımı orijinal sayıya eşitse, doğru bir ayrıştırma yapılmış demektir.

Asal çarpanlara ayırmanın bir diğer önemli kuralı, sıralamanın önemli olmamasıdır. Yani, asal çarpanların sırası, çarpımın sonucunu değiştirmez. Örneğin, 30 = 2 × 3 × 5 veya 30 = 3 × 5 × 2 şeklinde yazılabilir. Her iki ifade de aynı sonucu verir ve asal çarpanlar değişmez.

Asal Çarpanlara Ayırma Uygulamaları

Asal çarpanlara ayırma, matematiksel problemlerin çözümünde geniş uygulama alanlarına sahiptir. Bu yöntem, özellikle ortak bölenler ve katların bulunmasında kullanılır. İki sayının ortak asal çarpanları belirlenerek, bu sayılar arasındaki en büyük ortak bölen (EBOB) ve en küçük ortak kat (EKOK) hesaplanabilir.

Ayrıca, asal çarpanlara ayırma, şifreleme sistemlerinde önemli bir rol oynar. Özellikle RSA gibi modern şifreleme algoritmaları, büyük asal sayılar kullanılarak veri güvenliğini sağlar. Bu tür algoritmalar, asal çarpanlara ayırma işleminin zorluğundan yararlanarak, bilgilerin yetkisiz erişimlere karşı korunmasını mümkün kılar.

Asal çarpanlara ayırma, veri analizi ve bilgisayar bilimlerinde de yaygın olarak kullanılır. Büyük veri kümelerinin analizi sırasında, asal çarpanlara ayırma yöntemleri kullanılarak verilerin daha verimli bir şekilde işlenmesi sağlanır. Bu yöntem, algoritmaların optimizasyonu ve hesaplama hızının artırılması için önemli bir araçtır.